ΔΙΑΓΩΝΙΣΜΑΤΑ ΦΥΣΙΚΗΣ ΚΑΤ/ΝΣΗΣ Β ΛΥΚΕΙΟΥ

ΔΙΑΓΩΝΙΣΜΑΤΑ ΧΡΗΣΙΜΑ ΓΙΑ ΤΟΥΣ ΜΑΘΗΤΕΣ ΤΗΣ Β ΛΥΚΕΙΟΥ

Διαγωνίσματα στη φυσική Β΄Λυκείου Κατεύθυνσης by jbaganas

ΔΙΑΓΩΝΙΣΜΑ ΚΙΝΗΣΕΙΣ -ΝΟΜΟΙ ΝΕΥΤΩΝΑ

Διαγώνισμα στη φυσική Α΄ Λυκείου by jbaganas

ΔΙΑΓΩΝΙΣΜΑΤΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ

ΔΙΑΓΩΝΙΣΜΑΤΑ ΦΥΣΙΚΗΣ Γ΄ ΛΥΚΕΙΟΥ by jbaganas

ΦΥΣΙΚΗ ΠΑΝΕΛΛΗΝΙΕΣ 4ο ΘΕΜΑ

ΦΥΣΙΚΗ Γ΄ ΛΥΚΕΙΟΥ ΤΟ 4 ΘΕΜΑ by jbaganas

ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ 3ο ΘΕΜΑ

ΦΥΣΙΚΗ Γ΄ ΛΥΚΕΙΟΥ ΤΟ 3 ΘΕΜΑ by jbaganas

ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ 2ο ΘΕΜΑ

ΦΥΣΙΚΗ Γ΄ ΛΥΚΕΙΟΥ ΤΟ 2 ΘΕΜΑ by jbaganas

ΦΥΣΙΚΗ ΠΑΝΕΛΛΗΝΙΕΣ 1ο ΘΕΜΑ

ΦΥΣΙΚΗ Γ΄ ΛΥΚΕΙΟΥ - ΤΟ 1 ΘΕΜΑ by jbaganas

ΣΥΚΓΡΙΣΗ ΒΑΣΕΩΝ ΓΕΝΙΚΩΝ ΛΥΚΕΙΩΝ 2012

ΣΥΓΚΡΙΣΗ ΒΑΣΕΩΝ ΓΕΝΙΚΩΝ ΛΥΚΕΙΩΝ 2012 - 2011 90% by Dessi Siva

107 ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ Β ΓΥΜΝΑΣΙΟΥ

ΑΡΚΕΤΑ ΘΕΜΑΤΑ ΓΙΑ ΔΟΥΛΕΙΑ...

ΕΝΑ ΠΡΟΒΛΗΜΑ ΣΤΗΝ ΕΠΙΤΑΧΥΝΣΗ ΤΡΟΧΟΥ !!

Τροχός ακτίνας R = 2m ξεκινά τη χρονική στιγμή t = 0 να κυλίεται χωρίς ολίσθηση σε οριζόντιο δάπεδο με αcm = 2m/s2. Να υπολογίσετε τη χρονική στιγμή t = 2s το μέτρο της επιτάχυνσης: α) του ανώτερου σημείου του τροχού β) των σημείων της περιφέρειας του τροχού που βρίσκονται σε ύψος h = R γ) του σημείου επαφής του τροχού με το έδαφος. Για τη λύση της άσκησης πατήστε Επιτάχυνση σημείων τροχού που κυλίεται χωρίς ολίσθηση (Λύση)

ΘΕΜΑΤΑ ΠΑΝΕΛΛΗΝΙΩΝ(2002-2012)

Θέματα Πανελληνίων Γ Λυκείου ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ (έως και 2008) by Γιώργος Παπαδημητρίου

ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΣΤΙΣ ΤΑΛΑΝΤΩΣΕΙΣ

ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ by georgulo

ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ 2ο ΘΕΜΑ

ΦΥΣΙΚΗ Γ΄ ΛΥΚΕΙΟΥ ΤΟ 2 ΘΕΜΑ by jbaganas

ΘΕΩΡΙΑ ΚΑΙ ΑΣΚΗΣΕΙΣ

Mathimatika B Gymnasioy Theoria-Askiseis by taexeiola_blogspot

ΘΕΜΑΤΑ ΠΡΟΑΓΩΓΙΚΩΝ ΕΞΕΤΑΣΕΩΝ

ΘΕΜΑΤΑ ΠΡΟΑΓΩΓΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΓΙΑ ΜΑΘΗΤΕΣ Α ΓΥΜΝΑΣΙΟΥ

Μαθηματικά Α' Γυμνασίου (58 Διαγωνίσματα) by kats61

ΔΙΑΓΩΝΙΣΜΑΤΑ ΓΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ Α ΓΥΜΝΑΣΙΟΥ

ΜΙΑ ΣΕΙΡΑ ΔΙΑΓΩΝΙΣΜΑΤΩΝ ΓΙΑ ΤΟΥΣ ΜΑΘΗΤΕΣ Α ΓΥΜΝΑΣΙΟΥ,ΑΞΙΖΕΙ ΝΑ ΤΗΝ ΔΕΙΤΕ...

Διαγωνίσματα Α Γυμνασίου by Christopher Papanikolaou

ΒΟΗΘΗΜΑ ΦΥΣΙΚΗΣ

ΕΝΑ ΠΟΛΥ ΚΑΛΟ ΒΟΗΘΗΜΑ ΦΥΣΙΚΗΣ ΑΠΟ ΤΙΣ ΕΚΔΟΣΕΙΣ ΒΟΛΑΝΑΚΗ ΓΙΑ ΤΟΥΣ ΜΑΘΗΤΕΣ Β ΓΥΜΝΑΣΙΟΥ

Φυσική, Β΄ Γυμνασίου - Βολονάκη

ΒΙΒΛΙΟ ΒΟΛΑΝΑΚΗ ΑΛΓΕΒΡΑ Α ΓΥΜΝΑΣΙΟΥ

ΕΝΑ ΧΡΗΣΙΜΟ ΒΙΒΛΙΟ

Μαθηματικά Α' Γυμνασίου - Βολονάκη

ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ ΕΠΑΝΑΛΗΨΗ

ΜΑΘΗΜΑΤΙΚΑ Α ΓΥΜΝΑΣΙΟΥ by ΑΙΜΑ ΤΙΜΗ

μαθηματικα γ γυμνασιου

ΜΑΘΗΜΑΤΙΚΑ Γ΄ ΓΥΜΝΑΣΙΟΥ

'Ενα φυλλάδιο που περιέχει θεωρία,μεθοδολογία ασκήσεων και αρκετές άλυτες ασκήσεις.
ΠΑΤΗΣΤΕ ΕΔΩ

ΦΥΛΛΑΔΙΟ

Θέματα Φυσικής Γ Γυμνασίου

Θέματα Φυσικής Γ Γυμνασίου

21ΦΕΒ

Δημοσιεύω μια σειρά από Θέματα για την Φυσική της Γ Γυμνασίου, που θα μπορούσαν να αποτελέσουν θέματα Διαγωνίσματος.

Η ύλη που αντιστοιχούν οι ασκήσεις είναι στα κεφάλια Ταλαντώσεις – Κύματα  - Φως.

Θέματα Φυσικής Γ Γυμνασίου

ΓΙΑ ΚΑΛΟΥΣ ΛΥΤΕΣ

Test  

Γιατί όποιος ξέρει μπάνιο, κολυμπά και στα βαθιά...

ΤΑΞΗ Α΄

1.   Κινηματική: 1. 2. 3. 4. 5.

2. Δυναμική σε μια διάσταση: 1. 2. 3.  4. 5.    

3. Δυναμική στο επίπεδο: 1. 2. 3. 4.

4. Κυκλική κίνηση: 1. 2.

5. Οριζόντια βολή: 1.

6. Τριβή: 1. 2. 3.

7. Ορμή: 1. 2. 3.

8. Έργο - Ενέργεια: 1. 2. 3. 4.

9.  Διαγωνίσματα Εξετάσεων 1.

Περισσότερα από εδώ.

 ΤΑΞΗ Β΄

ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ

1. Αέρια: 1. 2. 3. 4.

2. Θερμοδυναμική: 1. 2. 3. 3ωρο. 4. 5.

3. Ηλεκτρικό πεδίο: 1. 2.

4. Μαγνητικό πεδίο 1.

5. 3ωρο Ηλεκτρικό - Μαγνητικό

6. Επαγωγή: 1. 2. 3. 4. 5.

7. Επαναληπτικό Διαγώνισμα 3ωρο

8.  Τελικό Εξετάσεων 1.

Περισσότερα από εδώ.

ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ

1.   Στατικός Ηλεκτρισμός: 1. 2. 3. 3ωρο

2. Συνεχές ρεύμα: 1. 2. 3.

3. Ηλεκτρομαγνητισμός: 1. 2.

4. Ταλαντώσεις: 1.

5. Επαναληπτικό Διαγώνισμα 3ωρο.

Περισσότερα από εδώ.

XHMEIA ΚΑΤΕΥΘΥΝΣΗΣ

1.   Θερμοχημεία 1. 2.

2. Διαγώνισμα κεφ.1-2. 1.

3. Χημική Κινητική. 1.

4. Χημική ισορροπία 1. 2.

5. Οξειδοαναγωγή 1. 2.

πηγη http://dmargaris.blogspot.gr/p/test.html¨

ΥΛΙΚΟ ΥΠΟΨΗΦΙΩΝ

Αγαπητοί υποψήφιοι-μαθητές.

Καλώς ήρθατε.

Εδώ θα βρείτε επεξεργασμένο υλικό που μπορείτε να χρησιμοποιήσετε για την προετοιμασία σας, εν όψει των εξετάσεών σας.

Στην Α΄ομάδα, θα βρείτε ερωτήσεις θεωρίας, κατάλληλες για Α΄και Β΄Θέμα.

Στην Β΄ομάδα ασκήσεις που καλύπτουν το αντίστοιχο υποκεφάλαιο, ξεκινώντας από τις πλέον εύκολες, προς δυσκολότερες.

Στην Γ΄ομάδα υπάρχουν γενικές ασκήσεις.

ΤΑΛΑΝΤΩΣΕΙΣ       

ΚΥΜΑΤΑ

ΜΗΧΑΝΙΚΗ

ΚΡΟΥΣΕΙΣ

ΤΕΣΤ ΘΕΡΜΟΔΥΝΑΜΙΚΗΣ

Ισοβαρής θέρμανση και αδιαβατική ψύξη.

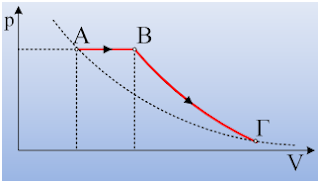
Μια ποσότητα αερίου βρίσκεται στην κατάσταση Α σε πίεση 4·10⁵Ν/m² και όγκο 5L. Απορροφώντας το αέριο θερμότητα 7000J, έρχεται ισοβαρώς στην κατάσταση Β, με όγκο 10L, από όπου ψύχεται αδιαβατικά μέχρι να αποκτήσει θερμοκρασία ίση με την θερμοκρασία στην κατάσταση Α, ερχόμενο στην κατάσταση Γ.

i) Να βρεθεί για το αέριο η γραμμομοριακή ειδική θερμότητα υπό σταθερή πίεση.

ii) Πόσο έργο παράγει το αέριο κατά την αδιαβατική εκτόνωση;

iii) Να βρείτε τον όγκο του αερίου στην κατάσταση Γ.

Δίνεται R=8,314J/mοℓ·Κ.                         

ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Β ΤΡΙΜΗΝΟ

Στο παρακάτω κύκλωμα ο διακόπτης δ είναι αρχικά ανοιχτός. Σε κάποια στιγμή κλείνουμε το διακόπτη. Τότε:

Α1) Ποιο από τα δύο αμπερόμετρα θα δώσει πρώτο ένδειξη και γιατί;

Α2) Ποιο από τα δύο αμπερόμετρα θα δώσει μεγαλύτερη ένδειξη και γιατί;

ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Γ ΓΥΜΝΑΣΙΟΥ

Θέμα 3^ο

3Α. Να βρεις τη γωνία ανάκλασης της ακτίνας στις παρακάτω περιπτώσεις:

                           

3B. Μια μονοχρωματική ακτίνα διαδίδεται αρχικά στον αέρα και κάποια στιγμή συναντά την ελεύθερη επιφάνεια νερού σε σημείο Σ, οπότε ένα μέρος της ανακλάται και το υπόλοιπο διαθλάται.

3Β.1. Ποια από τις πορείες (1), (2), (3) θα ακολουθήσει η διαθλώμενη ακτίνα;

3Β.2. Να σημειώσεις στην κόλλα το κατάλληλο σύμβολο ( =,  >  ή  < ) σε καθένα από τα παρακάτω κενά: 

i)   θ   …    α   , όπου θ η γωνία πρόσπτωσης και α η γωνία ανάκλασης.

ii)  α   …   δ   , όπου α η γωνία ανάκλασης και δ η γωνία διάθλασης.

iii) c_o  …   c   , όπου c_o η ταχύτητα της ακτίνας στον αέρα και c η ταχύτητά της στο νερό.

Μεταβολές αερίων. Ένα ακόμη test 2012-13

Ένα αέριο βρίσκεται σε  δοχείο, σε κατάσταση Α με όγκο 8L και πίεση 1·10⁵Ν/m². Από την κατάσταση αυτή μπορεί να έρθει αντιστρεπτά σε όγκο 1L, με τρεις τρόπους:

Α) μεταβολή ΑΒ ισοβαρώς,   Β) ΑΓ ισόθερμα         Γ) ΑΔ αδιαβατικά.

i)  Να παραστήσετε στο ίδιο διάγραμμα p-V τις τρεις παραπάνω μεταβολές.

ii) Πότε απαιτείται να προσφέρουμε περισσότερη ενέργεια μέσω έργου κατά την ισόθερμη ή κατά την αδιαβατική συμπίεση; Να δικαιολογήσετε την απάντησή σας.

iii) Αν κατά την ισοβαρή συμπίεση το αέριο αποβάλλει θερμότητα 1.750J, να υπολογίσετε το έργο και την μεταβολή της εσωτερικής ενέργειας στην μεταβολή αυτή.

iv)  Να υπολογίσετε για το αέριο το λόγο γ=C_p/C_v.

v)  Να βρείτε το έργο κατά την ισόθερμη μεταβολή.

ΣΥΝΔΕΣΜΟΛΙΑ ΑΝΤΙΣΤΑΣΕΩΝ

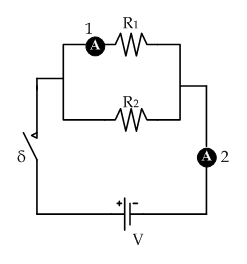
Αν ο καθένας από τους όμοιους αντιστάτες του διπλανού σχήματος έχει αντίσταση R= 38Ω, 

α. Να βρείτε την ολική αντίσταση του κυκλώματος.

β. Πως πρέπει να συνδεθούν οι αντιστάτες ώστε η τιμή της ολικής αντίστασης να πάρει την μέγιστη τιμή της και πως για να πάρει την ελάχιστη;

γ.  Πόση είναι σε κάθε περίπτωση η τιμή της ολικής αντίστασης;

Μια θερμική μηχανή και η απόδοσή της.

Το αέριο μιας θερμικής μηχανής διαγράφει τον κύκλο του διπλανού σχήματος, όπου η ΑΓ είναι αδιαβατική,  παράγοντας έργο 160J σε κάθε κύκλο. Η μηχανή στρέφεται με συχνότητα f=1000στρ/min.

i)  Να υπολογίσετε τη μεταβολή της εσωτερικής ενέργειας του αερίου στη διάρκεια της αδιαβατικής εκτόνωσης.

ii)  Υπολογίστε για το αέριο το λόγο γ=C_p/C_v.

iii) Πόση θερμότητα απορροφά η μηχανή και πόση αποβάλλει στο περιβάλλον σε μία ώρα;

Απάντηση:

TEST ΘΕΡΜΙΚΕΣ ΜΗΧΑΝΕΣ

Το αέριο μιας θερμικής μηχανής διαγράφει τον κύκλο του διπλανού σχήματος, όπου η ΓΑ είναι αδιαβατική. Δίνεται για την κατάσταση Α p_Α=8∙10⁵Ν/m² V_Α=4L, ενώ W_ΑΒ=9.600J. Όλες οι μεταβολές θεωρούνται αντιστρεπτές ενώ για το αέριο γ=3/2.

i)   Να βρείτε τον όγκο στην κατάσταση Β.

ii)  Να υπολογίσετε την θερμότητα που απορροφά το αέριο στην μεταβολή ΑΒ.

iii) Να βρείτε την πίεση του αερίου στην κατάσταση Γ.

iv) Αφού υπολογίσετε την θερμότητα Q_c που αποβάλει η μηχανή στη διάρκεια της κυκλικής μεταβολής, να βρείτε την απόδοσή της.

Μονάδες: 15+20+30+35=100

ΦΑΙΝΟΜΕΝΟ DOPPLER

Ένα τρένο κινείται ευθύγραμμα με ταχύτητα υ_s=34m/s. Πάνω του υπάρχει μια ηχητική πηγή που παράγει ήχο συχνότητας f_s=680Ηz, ενώ δυο επιβάτες Α και Β βρίσκονται εναλλάξ της πηγής, όπως στο σχήμα, ακίνητοι ως προς το τρένο.

i)  Ποιας συχνότητας ήχο ακούει καθένας επιβάτης;

ii)  Να βρεθεί το μήκος κύματος του ήχου που ακούνε οι δυο επιβάτες.

Δίνεται η ταχύτητα του ήχου υ=340m/s.

ΤΕΣΤ ΜΗΧΑΝΙΚΗ

Ένας κύλινδρος σε κεκλιμένο επίπεδο.

Γύρω από έναν ομογενή κύλινδρο μάζας Μ=2kg και ακτίνας R=0,1m έχουμε τυλίξει ένα αβαρές νήμα. Τοποθετούμε τον κύλινδρο σε κεκλιμένο επίπεδο κλίσεως θ, όπου ημθ=0,8 και τη στιγμή t₀=0 τον αφήνουμε να κινηθεί, ασκώντας σταθερή δύναμη μέτρου F=5Ν, στο άκρο Α του νήματος παράλληλη στο επίπεδο, όπως στο σχήμα. Αν ο κύλινδρος παρουσιάζει με  το επίπεδο συντελεστές τριβής μ=μ_s=0,25, για τη στιγμή t₁=1s, να βρεθούν:

i)  Η επιτάχυνση του κέντρου μάζας του κυλίνδρου και η μετατόπιση του άξονά του.

ii) Η ταχύτητα του κέντρου μάζας και η γωνιακή ταχύτητα του κυλίνδρου.

iii) η ισχύς κάθε δύναμης που ασκείται στον κύλινδρο.

iv) Οι ρυθμοί μεταβολής:

 α) της στροφορμής του κυλίνδρου, ως προς τον άξονα περιστροφής του.

 β) της κινητικής ενέργειας του κυλίνδρου.

 γ) της κινητικής ενέργειας λόγω περιστροφής του κυλίνδρου

Δίνεται η ροπή αδράνειας του κυλίνδρου ως προς τον άξονά του Ι_cm= ½ MR² και g=10m/s².

ΚΥΜΑΤΑ

Διάθλαση ή ολική ανάκλαση;

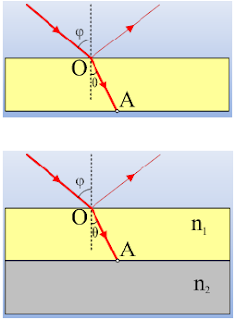
Μια μονοχρωματική ακτίνα φωτός προσπίπτει υπό γωνία φ σε μια γυάλινη πλάκα Α με δείκτη διάθλασης n₁. Η διαθλώμενη φτάνει στο σημείο Α.

i) Η ακτίνα στο Α, θα υποστεί:

   α) μόνο ανάκλαση 

   β) μόνο διάθλαση     

   γ) ανάκλαση και διάθλαση.

ii) Κάτω από την πλάκα αυτή, βάζουμε μια δεύτερη με διαφορετικό δείκτη διάθλασης n₂. Τότε η ακτίνα στο σημείο Α, θα υποστεί:

α) μόνο ανάκλαση               

β) μόνο διάθλαση       

γ) ανάκλαση και διάθλαση     

δ) εξαρτάται από την τιμή του δείκτη διάθλασης n₂.

Να δικαιολογήσετε τις απαντήσεις σας.

Ένα τεστ στις μηχανικές ταλαντώσεις. 2012-13

Τα σώματα Σ₁ και Σ₂ με μάζες m₁=4kg και m₂=2kg, ηρεμούν όπως στο σχήμα, στα άκρα δύο κατακόρυφων ελατηρίων με σταθερές k₁=k₂=100Ν/m, απέχοντας κατακόρυφη απόσταση d.

Εκτρέπουμε το Σ₁ κατακόρυφα προς τα πάνω κατά y₁=0,4m και κάποια στιγμή που θεωρούμε t=0, το αφήνουμε να κινηθεί.

i) Να αποδειχτεί ότι το σώμα Σ₁ θα πραγματοποιήσει ΑΑΤ.

ii) Να υπολογιστούν η περίοδος και η ενέργεια ταλάντωσής του.

iii) Αν τη στιγμή t₁=2π/15 s  το Σ₁ συγκρούεται πλαστικά με το σώμα Σ₂, να βρεθούν:

  α) Η αρχική απόσταση d των δύο σωμάτων.

  β) Η κινητική ενέργεια του συσσωματώματος, αμέσως μετά την κρούση.

  γ) Η ενέργεια ταλάντωσης του συσσωματώματος μετά την κρούση.

Θεωρείστε ότι τα δυο σώματα είναι αμελητέων διαστάσεων, οι άξονες των δύο ελατηρίων συμπίπτουν ενώ g=10m/s².